Defining
Excellence in Mathematics
Jonathan Zderad
Northwestern College
1. Introduction
The purpose of this essay is to identify standards by which mathematicians, teachers, and students can identify and encourage excellence in mathematics. I claim that certain standards of mathematics are almost universally accepted. Moreover, I also claim that there are two additional standards of mathematics, for which the Christian mathematician may further critique the mathematical discipline. Ultimately, I wish to advance a discussion of excellence in mathematics from a Christian perspective.
2. Beginning the
discussion
From an historical
perspective, there may seem to be much variability in how mathematics was (and
is) conducted from culture to culture and generation to generation, even
mathematician to mathematician. One
mathematician might value practical applications, specifically focusing on precise
algorithms that can be used to solve a wide variety of problems. Another mathematician might value rigorous
logical development and depth of analysis.
Another mathematician might value putting mathematics on a formal
foundation with “correct” notation.
Still another mathematician might value the beauty of mathematics and
the relationships between various fields of mathematics and other fields of
knowledge. As mathematics is being
developed, specifically to solve important problems of the day, universal
standards seem to be allusive. Yet, as
the dust clears and significant subfields of mathematics are left standing, I
argue that this knowledge is presented to the next generation in a predictable
manner.
A number of mathematicians
have attempted to describe what happens as mathematics develops. By looking at what each have written, we can
infer, sometimes directly and sometimes indirectly, what qualifies mathematics
as excellent.
Sawyer (1955) describes how
to develop mathematicians. Sawyer begins
by stating that “the desire to explore
[italics added] marks out the mathematician” (1955, p.19). He notes how the young mathematician (even in
grade school) will begin to be interested in patterns. But the mathematician is not satisfied with a
beautiful pattern. The mathematician
must attempt to explain why the
pattern occurs. Furthermore, the mathematician
will attempt to generalize
observations to as wide of a class of conditions as possible. Generalizations may show how two results are
related, by clarifying which result is the generalization of the other. In fact this allows a theorem to simplify ideas, to identify the really
important facts and avoid unnecessary computations. Sawyer claims that all of these activities of
a mathematician – exploring, explaining, generalizing, and even simplifying –
tend to expand the subject of mathematics.
But a mathematician also is attempting to unify separate results into one, resulting in a contraction of the
subject of mathematics. Sawyer is
focusing on qualities of an ideal mathematician; which I take to imply will
also be true of the excellent mathematics that is produced.
Polya (1954) describes the
process of doing mathematics. Polya
identifies three iterative processes. Generalization
is “passing from the consideration of a given set of objects to that of a
larger set” (p.103). Specialization is “passing from the
consideration of a given set of objects to that of a smaller set, contained in
the given one” (p.104). Reasoning from analogy involves identifying “similarity
on a more definite and more conceptual level” (p.104). Polya is focusing on aspects of inductive
reasoning; which I take imply characteristics of quality mathematics.
MacLane (1986) asks the
question “How does one evaluate the depth and importance of Mathematical
research?” (p. 3). After surveying the
content of mathematics, he lists what he considers to be the preferred and
overlapping directions for mathematical research in the future.
(a) Extracting ideas and problems from the
(scientific) environment,
(b) Formulating [italics added] ideas;
(c) Solving externally posed problems;
(d) Establishing new connections between Mathematical
concepts;
(e) Rigorous formulation of concepts;
(f) Further development of
concepts (e.g., new theorems);
(g) Solving (or partially
solving) internal Mathematical problems;
(h) Formulating new conjectures
and problems;
(i) Understanding aspects of all of the above. (pp. 449-450)
MacLane in focusing on his preferences
for the content of mathematical research; which I infer will describe
excellence in mathematical research.
Hardy (1984) comes very close
to what I am trying to accomplish. In
his defense of mathematics, Hardy devotes a good portion on “tests” that insure
the quality of mathematics. He states
that beauty, having the concepts “fit
together in a harmonious way” (p. 85), is the first test. He also elevates seriousness, “the significance of the mathematical ideas which it
connects” (p. 89), as a related and almost equally important test. He mentions generality, which is described as focusing on ideas that are “a
constituent in many mathematical constructs” (p.104). Hardy also mentions depth, nebulously described as digging deeply into the lower strata
of mathematical ideas (pp.110-111). The
implication is that there are well-recognized standards to separate quality
mathematics from the trivial, although these standards may be hard to formally
define.
2.1 Beauty
A mathematician, like a painter or a poet, is a maker
of patterns … The mathematician’s patterns, like the painter’s or the poet’s
must be beautiful; the ideas, like
the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent plane in the world for
ugly mathematics… It may be very hard to
define mathematical beauty, but that
is just as true of beauty of any kind – we may not know quite what we mean by a
beautiful poem, but that does not prevent us from recognizing one when we read
it. (Hardy, 1984, pp. 84-85)
To illustrate symbolical
beauty, look at the following mathematically equivalent (with respect to the
real numbers) representations of a particular function.
OR 
A number of questions come
to mind. Why is a square root symbol
more elegant that a fractional exponent.
Why avoid negative exponents? Why
is so much mathematical effort placed on “simplifying” results? The answer to these questions cannot be
computational advantage alone.
To illustrate conceptual
beauty consider the set {…, -10, -3, 4, 11, 18, …}. From a number theoretic perspective the set
can be viewed as solutions to the following congruence equation: 
. From an abstract
algebra perspective the set can be viewed as the equivalence class 
situated in the larger
group structure Z7. A number of questions come to mind. Which viewpoint leads more naturally to a
geometric understanding? Which viewpoint
helps to illuminate the symmetric properties of number sets? To which viewpoint is the mind more immediately
drawn?
To illustrate beautiful
proofs Hardy gives the examples of Euclid’s proof of the infinitude of primes,
Pythagoras’ proof of the irrationality of 
, Cantor’s proof of the uncountability of the real numbers,
and Fermat’s two square theorem (a prime is expressible as the sum of two
squares if and only if it is of the form 4m + 1). Hardy identifies beautiful proofs as being
unexpected (using surprisingly simply tools), inevitable (the consequences are
inescapable), and economical (simple and clear-cut).
2.2 Practicality
Hardy (1984) does note that
“pure mathematics” is practical when it provides tools for “applied
mathematics.” Hardy also notes that
“applied mathematics” has been used to help fight disease and raise life
expectancy, and yet at the same time has increased the horrors of war.
However, Hardy (p. 75)
claims that mathematics is not ultimately useful,
and is justified in having a life of its own.
This would seem to contradict biblical warnings to avoid knowledge that
leads to puffed-up pride without benefiting others (1 Cor. 8:1-3). So I will include practicality as a standard
of mathematics, even though Hardy did not.
The standard of practicality
is upheld when mathematics illuminates or solves a problem that arises in
everyday life or that is posed by another non-mathematical discipline. Practicality is evident when using Calculus to
estimate marginal profit, or using Abstract Algebra to describe the structure
of NH3, or using Statistics to infer characteristics of human
populations.
2.3 Connectedness
Connectedness is upheld when
a mathematician relates findings to other branches of mathematics, especially
earlier mathematics. Connectedness, as I
am using the term, is related to what Hardy (1984) calls significance, which he describes as:
…connected, in a natural and illuminating way, with a
large complex of other mathematical ideas.
Thus a serious mathematical theorem, a theorem which connects
significant ideas, is likely to lead to important advances in mathematics
itself and even in other sciences. (p. 89)
Linear Algebra is connected when it explains how
matrices can model complex number multiplication. Differential Equations is connected when it
explains how most elementary and special functions in common use are actually
cases of the hypergeometric function.
Abstract Algebra is connected when it claims that most mathematical
structures involve groups. Set Theory is
connected when it axiomatizes the fundamental concept of collections of objects. Category theory is connected when it
organizes most of mathematics under the function concept.
2.4 Rigor
The standard of rigor is
upheld when a mathematician strives to answer every conceivable why question raised
by a skeptic. Typically a mathematician
attempts to eliminate doubt with thorough logical arguments following from a
limited set of axioms (whether implied or stated explicitly). The standard of rigor is also upheld when a
mathematician gives exact answers and can demonstrate general methods of
solution. Definitions, theorems, and
solutions are explicitly and clearly stated and errors in approximations are
clearly identified. Furthermore, rigor
is upheld when striving to encapsulate mathematical concepts in universally
accepted mathematical symbols like å, ò , or p.
2.5 Depth
The standard of depth is
upheld when a mathematician addresses serious and difficult problems. Hardy (1984) writes:
It seems that mathematical ideas are arranged somehow
in strata, the ideas in each stratum being linked by a complex of relations
both among themselves and with those above and below. The lower the stratum,
the deeper (and in general the more difficult) the idea. (p. 110)
In other words, a theorem is deep if it requires
“boring much deeper” using the most powerful tools of modern mathematics. Depth can be manifested in the following
ways:
i)
Identifying
sufficient, as well as necessary, conditions for some relationship to
hold. This is evident in Calculus when
appropriate conditions for the existence of the constructed integral
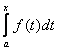
are given.
ii)
Identifying the
assumptions underlying a relationship.
This is evident in Topology when the concept of “connectedness” is
defined without reference to a metric.
iii)
Encapsulating a
large class of cases in a more general theorem.
This is evident in geometry when the Pythagorean Theorem is extended to
include other geometric figures (besides squares) constructed off of the sides
of a triangle.
Although Hardy is not approaching the discussion of standards of mathematics from a Christian perspective; nevertheless, his criteria would seem to be embraced by most Christian mathematicians. Now I wish to extend this discussion to include a Christian view of mathematics.
3. A Christian view of excellence
The main difficulty in developing a Christian view of mathematics lies in the fact that such an attempt necessitates using three separate, and often distinct, fields of knowledge. First, and possibly foremost, a Christian philosophy of mathematics is theological. Its assumptions lie at the heart of one’s understanding of God and His attributes. Solomon, in the book of Proverbs, describes the wisdom that comes from God. Wisdom, born of above, is personified in one of the most beautiful passages in all of scripture. There is deep mystery in what is written.
I, wisdom, dwell together with prudence; I possess knowledge and discretion… The Lord brought me forth as the first of his works, before his deeds of old; I was appointed from eternity, from the beginning, before the world began. When there were no oceans, I was given birth, when there were no springs abounding with water; before the mountains were settled in place, before the hills, I was given birth, before he made the earth or its fields or any of the dust of the world. I was there when he set the heavens in place, when he marked our the horizon on the face of the deep, when he established the clouds above and fixed securely the foundations of the deep, when he gave the sea its boundary so the waters would not overstep his command, and when he marked out the foundations of the earth. Then I was the craftsman at his side. I was filled with delight day after day, rejoicing always in his presence, rejoicing in his whole world and delighting in mankind. (Proverbs 8:12, 22-31)
This passage leads me into many investigations. Is God’s wisdom, among many other things, also quantitative in nature? Are geometric shape and algebraic relationships part of the craftsman at His side? Does the whole universe shout of His orderly measurements? Is mathematics part of the mystery of God?
Second, a Christian philosophy of mathematics must make statements about mathematics. It is obligated to describe what actually occurs in the formation and development of mathematics. Third, a Christian philosophy of mathematics is a philosophy. It must be “clearly formulated or rigorously reasoned about” (Frankena, 1964, p. 204). This demands careful definitions, especially of mathematics itself.
Even if one can weave the three fields of mathematics, philosophy, and theology cohesively, it is not obvious at all, or even necessarily desirable, that one will arrive at “the correct” Christian philosophy of mathematics. At the onset there may seem to be little from Christian theology that would help one get started, even to resolve the question of whether God is the originator of mathematics or, alternatively, whether mathematics is primarily a human activity. At first both seem possible and consistent within the Christian understanding of the nature of God.
There
are at least five competing philosophies of mathematics that have been
articulated within a Christian tradition (For a critique of fictionalism,
conceptualism, and creationism see Craig & Copan). These are encapsulated in the following five
claims:
A. Mathematics is a human linguistic phenomenon.
B. Mathematics is a description of God’s created
universe.
C. Mathematics exists in the mind of God.
D. Mathematics is a creative partnership between God and
humanity.
E. Mathematics is eternally created by God.
These various philosophies, as illustrated by claims
A-E, can be placed on a continuum based upon the ontological status given to
mathematics.
Low Ontological Status High Ontological Status
Fictionalism Descriptionism Conceptualism Co-creationism Creationism
Christian Fictionalism views mathematics
as linguistic expressions which have no reference to anything real. The statement “1 + 2 = 3” is taken as a
useful fiction which, though “true” given the rules of arithmetic, is
nevertheless vacuous. The numerals 1, 2,
and 3 are taken to have no ontological status.
However, the fictionalist still maintains that mathematical “practice
commits us to holding that certain statements are true according to the
standard account in the relevant area” (Copen & Craig, 2004, p. 181). Much of the previous discussion on standards
of mathematics would probably be dismissed by this viewpoint because Christian
Fictionalism sees mathematics as a humanly constructed linguistic game.
Christian Descriptionism views mathematics as a quantitative description of other
things created by God. Mathematics from
this view does not have a separate independent reality. Only God has an independent existence, and
mathematical objects (along with other abstract objects) are not one of the
things God has created. As Clouser (1991)
states, “the abstractions we arrive at … are never more – or less – that the
properties, relations, functions, etc,. of the quantitative aspect of things”
(p. 126). From this viewpoint the
standard of practicality is elevated. Christian
Descriptionism accepts that mathematics (including its abstractions) is a real
description of the universe, but gives mathematics no ontological status.
Christian Conceptualism views mathematics as emanating and existing in the
mind of God. Mathematics (along with
other abstract objects) proceeds from God’s mental actions and is sustained by
God. Mathematical objects are not created
beings, but rather are the concepts of God.
As Menzel (1990) states, “The idealized constructions that mathematics
is about are in fact actual in the divine intellect, and hence … the objects of
mathematics can be identified with divine constructions – God’s collectings and
concomitant concepts” (p. 93). Christian
Conceptualism still does not give mathematics ontological status, but it views
mathematical objects part of God’s mental activities.
Christian Co-creationism views mathematics as an active choice of reason by
God. God participates with and empowers
humanity to work out His quantitative purposes.
Mathematics reflects God’s creative artistry with aesthetic judgments
playing a fundamental role in the development of mathematics. As Case et al. (2005) note “…we participate
with God in the ongoing development of his creation and in the working out of
his purposes in the world” (p. 66). The
existence of a mathematical object begins the moment it is defined by humans;
hence mathematical objects are temporal.
Christian Co-creationism views mathematical objects as a cooperative
effort between God and humanity.
Christian Creationism views mathematics as coeternally existing in
dependence upon God (Howell & Bradley, 2001; Zderad, 2003). Mathematics in this view is necessary because
it involuntarily flows from God’s being.
Furthermore, mathematics has ontological status independent from the
physical/temporal universe. Christian Creationism
adds necessity and eternality to the conceptualist view of mathematics as God’s
mental activity.
The above discussion of Christian philosophies is germane because the issue of excellence in mathematics may be approached from different perspectives depending on one’s viewpoint of mathematics. Nevertheless, my purpose is not to critique these various Christian philosophies. Rather, I will attempt to show that much agreement can be reached by Christians on the discussion of excellence in mathematics (although from the fictionalist perspective talking about standards in mathematics may be meaningless). Whether mathematics is afforded ontological status or not, God is still the absolute standard of goodness in mathematics. Mathematics that is right is that which glorifies God and reflects his character.
There are many “standards”
of the Christian faith, which are summarized in the Ten Commandments (Exodus
20:1-17), the Sermon on the Mount (Matthew 5-7), and the Fruit of the Spirit
(Galatians 5:22-23). Ephesians 4:14-15
gives us a starting point:
Then we will no longer be infants, tossed back and
forth by the waves, and blown here and there by every wind of teaching and by
the cunning and craftiness of men in their deceitful scheming. Instead, speaking the truth in love [italics
added], we will in all things grow up into him who is the Head, that is,
Christ.
3.1 Mathematics
that is Loving
When asked “Which is the greatest commandment in the Law?” (Matthew 22:36), Jesus responded with “Love the Lord your God with all your heart and with all your soul and with all your mind” and “Love your neighbor as yourself” (Matthew 22:37, 39). Christian teaching usually addresses loving God with the heart (with one’s will, one’s desires, and one’s volition through obedience) and with the soul (with one’s very essence and personhood through a personal relationship with God).
But what does it mean to love God with one’s mind? Sire (1990) described what it means to love God with the ways in which we think. Sire claims that the Christian mind goes through both formation and reformation. Formation involves studying the scripture to answer life’s difficult questions, reading what other Christians have written, and obeying what the Bible says. Reformation involves challenging previous beliefs, seeking to grow in our understandings, and testing our beliefs against experience.
Formation and reformation, likewise, occur as Christian mathematicians delve into the intricacies of abstract objects. The ultimate purpose is so Christians studying mathematics will grow in personal relationship with God. Mathematics should seek the ultimate good of others, both in terms of its application and its explanation. Veatch (in Howell and Bradley, 2001, pp. 244-245) argues that the value of a mathematical project should be measured by the number of people influenced by the work, the benefits to broader fields of knowledge, and the benefits to the larger non-mathematical community. Mathematics should produce a better society and should lead to greater discernment as one is taught mathematics and as one investigates mathematics. Mathematics that dehumanizes should be rejected, especially that which relegates the study of people to the purely quantitative (Frankena, 1964). Furthermore, mathematicians should not be aloof, arrogant, or overly mysterious in their presentations of concepts. This means that mathematics teachers need to balance the needs of students with the mathematical standards of formality and rigor. The standards of formality and rigor can be burdensome for the amateur mathematician, and the mathematics teacher needs to carefully lead the student from the informal to the formal and from the intuitive to the profound.
3.2 Mathematics
that is Truthful
Mathematicians should be
aware of the truth claims that they are making.
Veatch (in Howell and Bradley, 2001, pp. 245-246) argues that
mathematics should focus on what is truly fundamental, which can be evidenced
by problems that:
1) are stated in ways
accessible to non-specialists,
2) necessarily require
mathematical machinery, and
3) illuminate the nature of
mathematics.
There are two extremes to be avoided. The first extreme is to only admit mathematics
that is immediately practical. If all
mathematical research was done for practical reasons alone at least two
negative results would probably occur.
First, mathematics would lack unity because researchers would not be
looking for commonalities among applications and methods. Second, without valuing the explanatory
nature of mathematics as it relates to creation and its Creator, mathematical
research might degrade into a means of controlling human behavior.
The other extreme is to
focus entirely upon mathematical abstraction.
There is something to be learned by comparing the 19th
century fascination with abstraction in both art and mathematics. Shaeffer (1968) traces the increased
abstraction in the art of Van Gogh, Gauguin, Cézanne, Picasso, and Mondrian. He claims that because these artists could
not find rational meaning in particular subjects, they began searching for a
universal principle that would bring meaning.
These “universals” included the noble savage (Gauguin), geometric form
(Cézanne), womanhood (Picasso), and structure (Mondrian). The logical progress of abstraction in art
leaves the viewer with no subject matter, no communication with the artist, and
finally no room for self. The similar
danger in mathematics is that through the desire for universal principles and
subject unity, we abstract axiomatic systems to such a point that the
mathematician cannot explain subject matter, and cannot relate findings to
anything in the physical universe. There
is meaning in particulars and the mathematician should not lose sight of them.
Axioms should eventually be chosen because of their correspondence with reality, both material and immaterial, not simply to play a logical game. Mathematics should avoid conclusions that are logically true, but meaningless. This standard, however, is not as stifling as it might first appear. Much of mathematics that was once viewed as “Fantasy” – imaginary numbers, infinite quantities, and hyperbolic geometry, for instance – has been demonstrated to correspond profoundly with aspects of the physical universe. This standard provides much freedom to engage in further mathematical discoveries, but does provide a check to avoid mathematics simply for its own sake. Furthermore, since God is the author of all knowledge, knowledge must have an underlying coherence (Howell and Bradley, 2001, pp. 248-249). We as mathematicians should seek to make sense of mathematics in light of the truths of theology, science, art, and literature.
4. Conclusions
Historically accepted mathematical standards are, at least on face value, in agreement with biblical principles in fundamental ways. The standard of beauty may reflect how we relate to and worship God. The standard of practicality may reflect how we are to relate to other humans made in God’s image. The standard of connectedness may reflect our desire for a coherent view of God’s reality. The standards of rigor and depth may reflect God’s value of our hard work. Thus a Christian view of mathematical excellence seems to affirm the value of mathematics as it has been historically developed. However, the Christian would probably put different emphasizes on particular standards. Moreover, the Christian will almost certainly uphold additional mathematical standards, such as truth and love, which are often ignored in wider mathematical circles.
Bibliography
Case, J.,
Clouser, R. A. (1991). The
Myth of Religious Neutrality. Notre
Dame, IN:
Frankena, W. K.
(1964). Love and Principle in Christian
Ethics. In A. Plantinga (Ed.), Faith
and Philosophy,
Hardy, G. H.
(1984). A Mathematician’s Apology.
Howell, R. W.
& Bradley, W. J. (2001). Mathematics
in a postmodern age: a Christian perspective.
MacLane, S. (1986). Mathematics form and function,
Menzel, C. (1990). Theism, Platonism, and the Metaphysics of
Mathematics. In M. Beaty (Ed.) Library of Religious Philosophy. Notre
Dame:
Polya, G. (1998).
Induction and analogy in mathematics.
In T. Tymoczko (Ed.), New
directions in the philosophy of mathematics (pp. 103-124).
Saywer, W. W. (1961).
Prelude to mathematics.
Shaeffer, F. A. (1968). The God
who is there,
Sire, J. W. (1990). Discipleship of the mind,
Zderad, J. A. (2003). Creationism – A Viable Philosophy of
Mathematics. In G. Crow & M. Zack
(Eds.), Fourteenth conference of the
Association of Christians in the Mathematical Science, 98-109.
Scripture taken from the HOLY BIBLE, NEW INTERNATIONAL VERSION®. Copyright © 1973, 1978, 1984 International Bible Society. Used by permission of Zondervan Publishing House.